Diagonaliztion.2

Diagonalization :: 대각화

n*n mattix A가 eigenvalues λ₁,  λ₂, …, λₙ 을 가지고 있고, 서로 독립된 eigenvector x₁, x₂, …, xₙ 을 가지고 있다고 가정하자. ((λᵢ, xᵢ)는 eigenpair)

S = [x₁ x₂ … xₙ], Λ = diag(λ₁, λ₂, …, λₙ)라 하면 S⁻¹AS = Λ

증명.

AS = A[x₁  x₂  …  xₙ]

      = [A*x₁  A*x₂  …  A*xₙ]

      = [λ₁*x₁  λ₂*x₂  …  λₙ*xₙ]

      = SΛ

 

Difference Equation :: 등차 방정식

일반적으로 uₖ₊₁ = A*uₖ는 다음의 단계로 풀 수 있다.

1. A의 독립 eigenvector로 이루어진 matrix S를 찾는다.
2. C = S⁻¹*u₀을 만족하는 C를 찾는다.
3. uₖ = c₁*λ₁ᵏ*x₁ + … + cₙ*λₙᵏ*xₙ으로 나타낸다
4. Aᵏ = S*Λᵏ*S⁻¹
5. uₖ = S*Λᵏ*S⁻¹*u₀
6. uₖ = S*Λᵏ*C
7. uₖ = Λᵏ*u₀

 

EX. 피보나치 수열

• 피보나치 행렬 u에 대해 정의

• 행렬 A에 대해 정의

• A의 eigenvalue 구하기

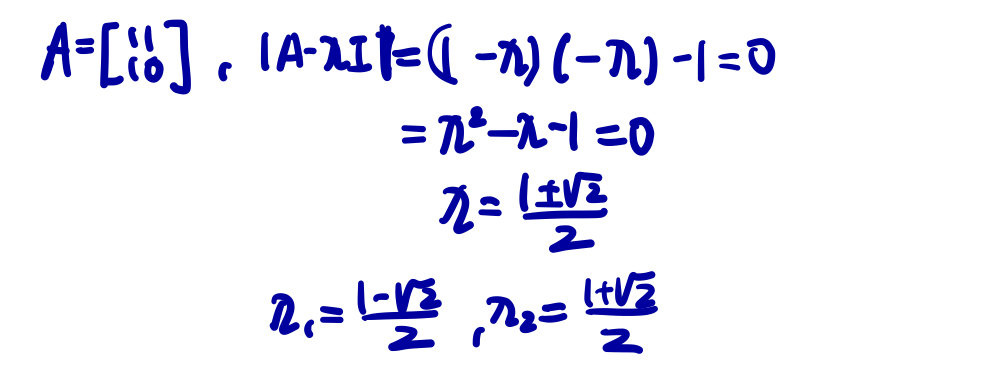
• 위의 구한 것들을 토대로 피보나치수열 정의

위의 정의는 diagonalization을 쓰지 않았지만 diagonalization을 쓰고도 정의가 가능함