Determinants.1

Determinants :: 행렬식

AB = I → 언제 B의 역행렬이 존재하냐?

숫자의 세계 : ab = 1 → a = ~0 이면 성립

행렬의 세계 : AB = I → det = ~0 이면 B의 역행렬 존재

matrix invertible ↔ determinant nonzero

determinant는 square matrix에 대해서만 정의됨

determinant of A : det A, |A|

 

정의

1. |A| = 1 if A is the identity
2. |A| = |(original A)| = -|(row exchanged A)|
   1. 한번 행이 바꿀때마다 부호가 바뀜
3. det [a1 a2 … taj … an]’ = tdet* [a1 a2 … aj … an]’, 모든 j에 대해*
4. det [a1 a2 … aj + bj … an]’ = det [a1 a2 … aj … an]’ + det [a1 a2 … bj. … an]’, 모든 j에 대해

정의 4 예시

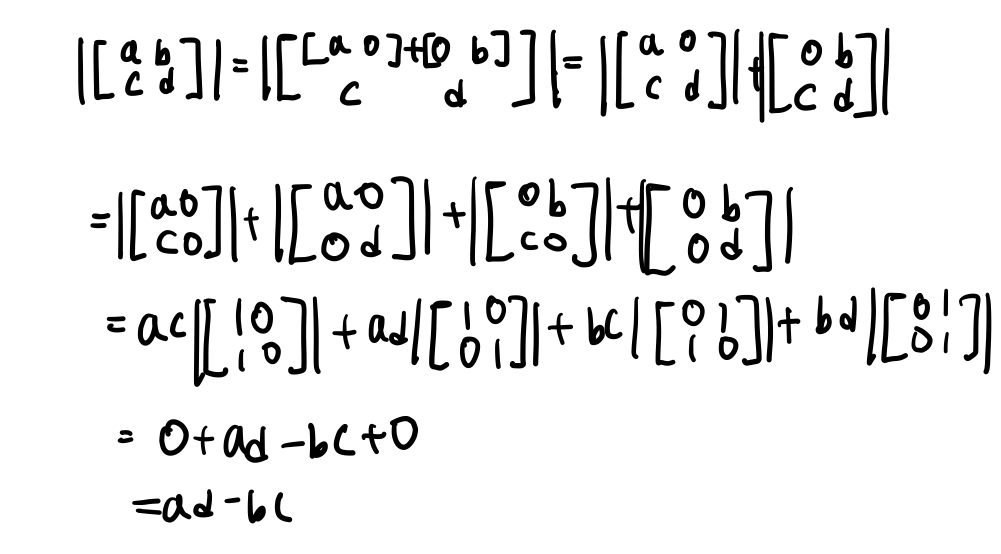
5. A가 같은 행을 가지고 있다면 |A| = 0

정의 5 예시

1. |A| = ab - ab
2. |A| = -|row exchanged A||A| = 0 (Definition 2)
3. |A| = -|A|

6. 어떤 row에 다른 어떤 row에 임의의 수를 곱하고 빼도 |A|는 변하지 않음

정의 6 예시

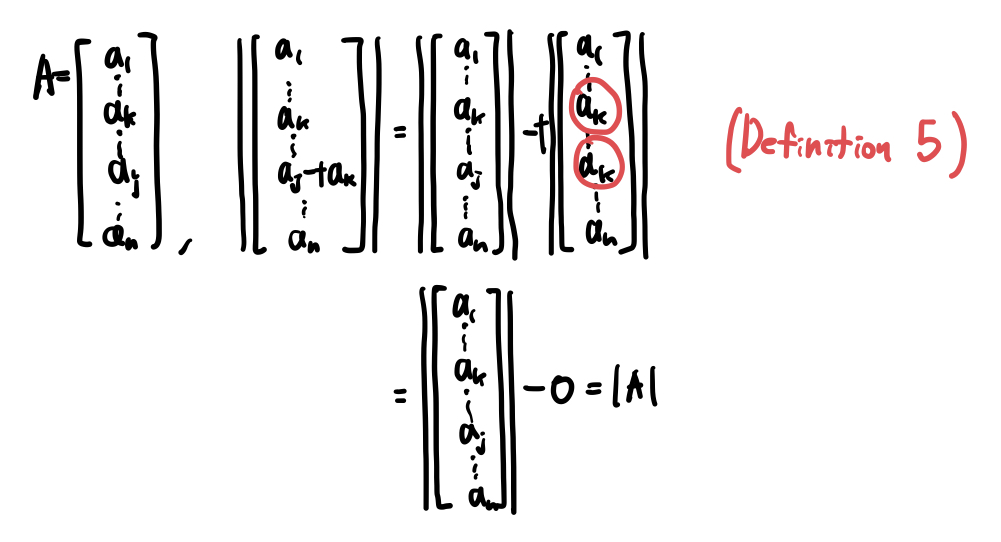
7. A가 0인 행을 가지고 있으면 |A| = 0

정의 7 예시

8. A가 triangular 하다면 |A| = a11a22a33 … ann

9. A가 invertaible한것과 |A| = ~0은 필요충분조건이다

10. A가 invertible하려면 n개의 pivots을 가지고 있어야함 ↔ det A = ~0

11. |A*B| = |A| * |B| (⇒ |(A의 역)| = 1 / |A|)

1. PA = LU (P = permutation)

12. |A'| = |A|