수학/선형대수학
Gram-Schmidt Process.2
implement
2022. 12. 22. 12:00
728x90

Gram-Schmidt Process
세개의 독립된 벡터 : v1, v2, v3
- orthogonal vector w1, w2, w3 생성
- w1 = v1
- w2 = v2 - (w1'v2/w1’w1)w1
- w3 = v3 - (w1’v3/w1’w1)w1 - (w2’v3/w2’w2)w2
- 새로운 벡터에 전 단계에서 만든 orthogonal 벡터에 projection한 벡터를 빼면 됨
- w1, w2, w3를 정규화한 q1, q2, q3 생성
- q1 = w1/||w1||
- q2 = w2/||w2||
- q3 = w3/||w3||
QR Factoriztion :: QR 분해
m*n 독립 행 matrix A에 대해 Gram-Schmidt process한 Q와 그로 인해 만들 수 있는 n*n invertible triangular matrix R 이 있다면 A = QR
A = (v의 outhonomal vecters)*(invertible n*n upper triangular matrix)
Gram-Schmidt process로 인해 생성된 matrix : Q

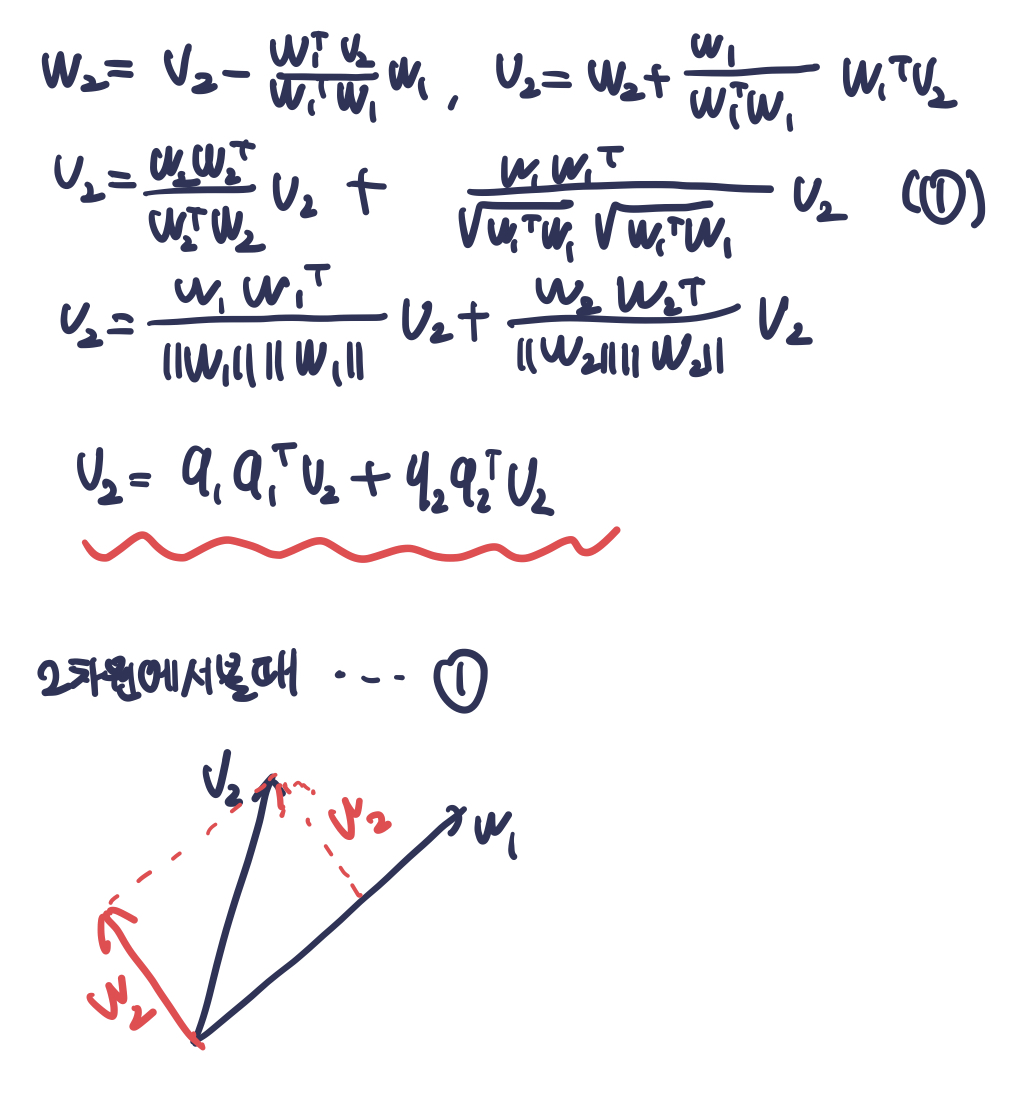
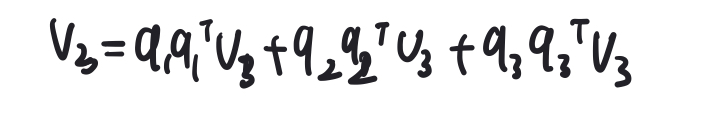
따라서

이를 이용하면 Ax = b의 해를 쉽게 구할 수 있다.
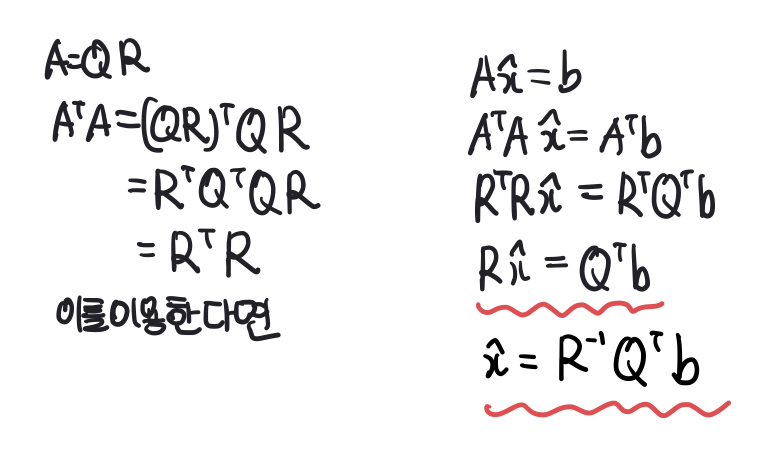
반응형